Blog

Cubic Gauss Sums

In the realm of number theory and mathematical marvels, Cubic Gauss Sums stand as captivating entities that have intrigued mathematicians for centuries. These intriguing mathematical constructs, named after the famous mathematician Carl Friedrich Gauss, unveil profound connections between number theory, complex analysis, and algebraic structures. In this article, we will embark on a journey to unravel the mysteries of cubic Gauss sums, exploring their definition, properties, and the remarkable insights they offer into the intricate world of mathematics.

Understanding Cubic Gauss Sums: Definition and Notation
A cubic Gauss sum refers to a particular type of mathematical expression that arises in the study of quadratic characters and Gauss sums. Let’s denote a cubic Gauss sum as $G(\chi)$, where $\chi$ represents a nontrivial character modulo a prime number $p$. Mathematically, the cubic Gauss sum can be expressed as:

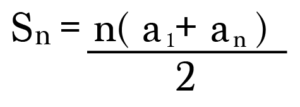
[G(\chi) = \sum_{x=1}^{p-1} \chi(x) e^{2\pi i x^3/p}]

In this equation, $\chi(x)$ represents the quadratic character evaluated at $x$, while $e^{2\pi i x^3/p}$ denotes the complex exponential function. The summation extends over all values of $x$ from 1 to $p-1$. The cubic Gauss sum encapsulates the interplay between quadratic characters and the cubic power function, offering deep insights into the behavior of these mathematical entities.

Exploring Properties and Patterns of Cubic Gauss Sums
Cubic Gauss sums possess fascinating properties and intricate patterns that have captivated mathematicians throughout history. Let’s delve into some notable aspects of these mathematical constructs:

1. Quadratic Characters and Symmetry
Cubic Gauss sums intimately connect with quadratic characters, which are fundamental in number theory. Quadratic characters are complex-valued functions defined modulo an odd prime $p$ that exhibit certain symmetries and periodicities. Cubic Gauss sums leverage these symmetries and encapsulate the behavior of quadratic characters in the context of cubic power functions.

2. Relationships with Other Gauss Sums
Cubic Gauss sums establish intriguing relationships with other types of Gauss sums, such as quadratic Gauss sums and quartic Gauss sums. These connections shed light on the deeper structure of Gauss sums and provide avenues for exploring the interplay between different mathematical entities.

3. Analytic Properties and Distribution
Cubic Gauss sums possess remarkable analytic properties, including their connection to complex analysis and the theory of modular forms. These mathematical constructs exhibit intricate distribution patterns, which have been extensively studied to understand their behavior across different prime values.

Applications in Number Theory and Beyond
The study of cubic Gauss sums transcends its intrinsic mathematical beauty and finds applications in various branches of number theory and related fields. Let’s explore a few key areas where cubic Gauss sums play a significant role:

1. Diophantine Equations and Rational Points on Elliptic Curves
Cubic Gauss sums provide insights into Diophantine equations and the distribution of rational points on elliptic curves. These mathematical constructs allow researchers to explore the solvability of certain equations and investigate the presence of rational solutions within specific mathematical structures.

2. Cryptography and Number-Theoretic Algorithms
The properties and relationships of cubic Gauss sums have implications in the field of cryptography and the development of number-theoretic algorithms. The study of these mathematical constructs contributes to the design and analysis of cryptographic protocols, ensuring the security and efficiency of modern communication systems.

3. Algebraic Number Theory and Galois Representations
Cubic Gauss sums intersect with algebraic number theory and the theory of Galois representations. These connections provide valuable insights into the behavior of algebraic numbers, field extensions, and the intricate interplay between algebraic structures and number-theoretic phenomena.

The Unending Quest: Exploring Cubic Gauss Sums
Cubic Gauss sums continue to fascinate mathematicians, serving as a testament to the profound beauty and complexity of mathematics. As researchers delve deeper into the intricacies of these mathematical constructs, new discoveries and insights emerge, unraveling the mysteries of number theory and beyond.

So let us embark on this unending quest, exploring the captivating world of cubic Gauss sums and unveiling the mathematical wonders that await us. With each step, we inch closer to a deeper understanding of the intricate patterns and connections that shape the vast landscape of mathematics.

Open Questions and Future Directions
Despite significant progress in understanding cubic Gauss sums, several open questions and avenues for further exploration remain. Mathematicians and researchers continue to delve into the depths of these mathematical constructs, aiming to uncover new insights and establish deeper connections. Some of the ongoing research directions include:

1. Higher-Dimensional Analogues
Generalizing cubic Gauss sums to higher dimensions is an area of active investigation. Exploring the properties and behavior of higher-dimensional Gauss sums could unveil new perspectives and deepen our understanding of the intricate relationships between number theory, algebra, and complex analysis.

2. Computational Aspects
Developing efficient algorithms for computing cubic Gauss sums and understanding their computational complexity is an important research direction. The ability to compute these sums with greater efficiency can open up new possibilities for their application in cryptography, computational number theory, and related areas.

3. Connection to Other Branches of Mathematics
Further exploring the connections between cubic Gauss sums and other branches of mathematics, such as representation theory, modular forms, and algebraic geometry, is an intriguing research avenue. Uncovering deeper connections and establishing bridges between different mathematical disciplines can lead to new insights and foster interdisciplinary collaborations.

Conclusion: Unveiling the Intricacies of Cubic Gauss Sums
In the realm of number theory and mathematical exploration, cubic Gauss sums stand as captivating mathematical entities that offer profound insights into the interplay between quadratic characters, complex analysis, and algebraic structures. Their properties, patterns, and applications have fascinated mathematicians for centuries.

As researchers continue to unravel the intricacies of cubic Gauss sums and explore their connections to various branches of mathematics, we are poised to gain deeper insights into the fundamental nature of numbers and uncover new mathematical vistas. The journey to understand these mathematical marvels is an ongoing one, with each step revealing new wonders and paving the way for future discoveries.

So let us embrace the beauty and elegance of cubic Gauss sums, for they hold within them the potential to unravel the mysteries of the mathematical universe and inspire generations of mathematicians to come.